
Work3 - Work3 First Order and Second Order System Analysis



ทบทวนสมการ Transfer Function ของ First Order System

Input เป็น Unit Step
จะได้ Output ของ First Order System เป็นเส้นโค้งเริ่มที่ 0 ไม่มี delay
สมการ Transfer Function ของ First Order System
q1 เป็นอัตราการไหลของนำ้เข้าถัง
q2 เป็นอัตราการไหลของนำ้ระบายออกจากถัง
A1 เป็นพื้นที่หน้าตัดของถัง h เป็นความสูงของระดับนำ้
สมการ Transfer Function ของระดับนำ้ที่เปลี่ยนแปลงเมื่อมีการเปิดวาล์วให้นำ้ระบายออก
กราฟของ system เป็นเส้นโค้งเมื่อเปิดวาล์วให้นำ้ระบายออก
สมการ และกราฟของ system เปลี่ยนเป็น Ramp หรือ เป็น integrator เมื่อปิดวาล์วไม่ให้นำ้ระบายออก

วงจรภายใน OP-AMP
แรงดัน Input เข้าที่ขา (-) ของ OP-AMP เป็น Unit Step มี่ค่า 5V/6V
กราฟสีดำเป็นกราฟแรงดัน Output ของ Unit Step 5V ไต่ขึ้นเป็น Ramp (Integrator) ขึ้นเรื่อยๆจนเท่ากับแรงดันไฟเลี้ยง 15V ซึ่ง Time constant จะมีค่าเท่ากับ 4.7ms ได้จากการคำนวณหรือวัดที่กราฟที่ 63% ของแรงดันสูงสุด ส่วนกราฟสีนำ้เงินเป็นกราฟของ Unit Step 6V ซึ่งมีลักษณะเดี่ยวกัน Time Constant เท่ากันแต่จะไต่ขึ้นเร็วกว่า Unit Step 5V
ในวงจรถ้าให้ R = 10KOhm , C = 0.47µF, ค่า Time constant จะได้เท่ากับ 4.7ms

สมการ Transfer Function ของ วงจร Integrator เป็น First Order System
กราฟของ system integrator ที่มี input เป็น Unit Step, Output เป็น Ramp เริ่มที่ 0 ไม่มี delay
การเอาวงจร integrator มาต่อแบบมี Feedback ป้อนกลับ

สมการ และ กราฟของ system integrator ที่มี Feedback ป้อนกลับ Output เป็นเส้นโค้งขึ้นที่ 0 ไม่มี delay
รูปแบบของวงจร system integrator ที่มี Feedback ป้อนกลับ ซึ่งใช้ OP-AMP อยู่ 3 ตัว โดยนำ Output จาก Op-AMP ตัวที่ 2 มากลับสัญญาณโดยต่อเข้า OP-AMP ตัวที่ 3 แล้วเอาสัญญาณ Output จาก OP-AMP ตัวที่ 3 นั้นมา Feedback เข้า OP-AMP ตัวที่ 1
การแปลงวงจรที่ใช้ OP-AMP 3 ตัว ยุบให้เหลือตัวเดียวแต่ยังคงทำงานเหมือนเดิม

สมการ Transfer Function ของ วงจร Integrator ที่มี Feedback ป้อนกลับ
KT คืออัตราการขยาย หรือ Proportional Gain ของระบบ
T2 คือ Time Constant ของวงจรซึ่งหาได้จากค่า R2 และ C ของวงจร
การวิเคราะห์ Second Order System
Input เป็น Unit Step
เอา Output U01จาก System ที่ 1 มาเข้าอีก System หนึ่งซึ่งเหมือนกับอันแรก

Output U02 ขอ�ง Second Order System จะเหมือนกับ First Order System แต่มีการ Delay ไม่ขึ้นที่ 0
สมการ Transfer Function ของ Second Order System หาได้โดยการเอาสมการของ System ที่ 1 มาคูณกับสมการของ System ที่ 2
แต่ Standard Form ของ Second Order System นั้นมีรูปแบบดังที่เขียนไว้ เราจะหาความสัมพันธ์ระหว่างสมการข้างบนกับสมการ Standard Form ของมัน
ω0 หรือ ωn คือความถี่ธรรมชาติของระบบๆหนึ่งซึ่งแต่ละระบบจะมีค่าที่ต่างกัน

จากการแก้สมการ เราได้ค่า D ซึ่งเป็น Damping Coefficient ของระบบ
ค่าของ Damping Coefficient อาจมีอยู่ 3 กรณี คือถ้า D=1 จะเป็น Critical Damp หรือจุดวิกฤต ซึ่งอาจจะแบ่งออกเป็นอีก 2 กรณีคือ Over Damping และ Under Damping
แต่ถ้าหากว่าค่า D มากกว่า 1 จะเป็นกรณี Overdamping



การหาราก (Root) ของสมการโดย Pole-Zero Plot
การหาราก (Root) ของสมการเราต้องให้ Denominator ของมันเท่ากับ 0 แล้วแก้หรือย้ายสมการเพื่อที่จะหา Root
การ plot ค่า root ของสมการ (ค่า S) บนพิกัด (Im,Re)
Im = Imagination
Re = Real
การหาราก (Root) ของสมการ Transfer Function (ค่า S) ของ Second Order System โดยจะให้ Denominator ของสมการเท่ากับ 0 แล้วหาคำตอบของสมการโดยใช้วิธีหา Solution ของสมการกำลังสอง
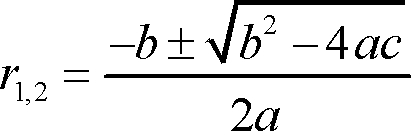
ราก (Root) ของสมการที่หาได้
ค่าของ Damping Coefficient จะมีอยู่ 3 กรณี คือถ้า D>0, D=1 และ D<1
ถ้า D>0 root ของสมการ (s1, s2) จะเป็นค่าจำนวนจริง (Real Root) กราฟของระบบจะเป็นดังในรูป
ถ้า D=1 root ของสมการ (s1, s2) จะเป็นค่าจำนวนจริง (Real Root) โดย s1 จะเท่ากับ s2 หรือเป็น Double root กราฟของระบบจะเป็นดังในรูป
ถ้า 0<D<1 root ของสมการ (s1, s2) จะเป็นค่าจำนวนเชิงซ้อน (Complex conjugated Root) กราฟของระบบจะเป็นดังในรูป
ถ้า D=0กราฟของระบบจะเป็นดังในรูป จะเป็น Continuous Oscillator หรือ Amplifier ซึ่งเป็นกรณีที่เกิดขึ้นยาก
การวิเคราะห์วงจร Integrator (First Order System)
การวิเคราะห์การเปลี่ยนแปลงระดับนำ้โดย First Order System
การวิเคราะห์วงจร Integrator แบบมี Feedback ส่งสัญญาณป้อนกลับ